Caracterizando la resolución de problemas desde la variación y el cambio en dominios discretos y la teoría fundamentada

Resumen

El estudio tuvo como propósito dar respuesta a la pregunta de investigación, ¿Cómo es la naturaleza de la resolución de problemas que involucran ecuaciones lineales diofánticas de la forma 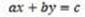    manifestado por profesores de matemáticas en formación? El trabajo estuvo orientado por un enfoque cualitativo con un diseño desde la teoría fundamentada. Como fuentes de datos se diseñaron e implementaron 6 actividades didácticas y una entrevista retrospectiva no estructurada a un grupo de 15 estudiantes que se forman para ser profesores de matemáticas. Entre los hallazgos se destacan las acciones variacionales manifestadas por los participantes, que les posibilitó ir de sustituciones y combinaciones variacionales a establecer relaciones para formalizar, generalizar, probar, organizar y reorganizar su conocimiento. El método de comparación constante, junto a los procesos de codificación (abierta, axial y selectiva), el muestreo y saturación teórica se constituyeron en la vía para interpretar y dar sentido a los datos posibilitando caracterizar la resolución de problemas en dominios discretos como un flujo permanente de acciones e interacciones entre procesos y subprocesos cuando los participantes resuelven problemas que involucran ecuaciones lineales diofánticas de la forma .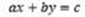