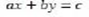Characterizing problem solving from variation and change in discrete domains and grounded theory

Abstract

The had as purpose answering the research question: What is the nature of problem solving involving linear diophantic equations of the form 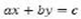as expressed by mathematics teachers in training? The project was guided by a qualitative approach with a grounded theory de- sign. As data sources, 6 didactic activities and a retrospective unstructured interview with a group of 15 students who are pursuing a mathematics teaching bachelor’s degree were designed and implemented. Among the findings, the variation- al actions expressed by the participants stud out, which enabled them to go from substitutions and variational combinations to establishing relationships in order to formalizing, generaliz- ing, testing, organizing and reorganizing their knowledge. The constant comparison method, together with code processing (open, axial and selective), sampling and theoretical saturation, became the way to interpret and make sense of the data, making it possible to characterize problem solving in discrete domains as a per- manent flow of actions and interactions between processes and sub-processes when the partici- pants solve problems involving linear diophantic equations of the form